Mathematics can feel like a puzzle at times, especially in Class 9 when concepts start building on each other like bricks in a tower. Whether you’re grappling with polynomials, unraveling the mysteries of Euclid’s geometry, or calculating surface areas, having a reliable formula sheet is like having a superpower. That’s why we’re thrilled to bring you this comprehensive Class 9 Maths Formula Sheet from A2zly team. This isn’t just a list—it’s a roadmap to mastering the CBSE syllabus, packed with key definitions, theorems, identities, and examples to make revision quick and effective.
At A2Zly, we believe education should be accessible and fun. We’ve proofread, decorated, and formatted this sheet for easy reading on your blog or study notes. Dive in, bookmark it, and let’s turn those tricky chapters into triumphs! Ready to launch your maths journey?
Table of Contents
🔢 Number System ➗

📊 Polynomials 🧮

🗺️ Co-ordinate Geometry 📍
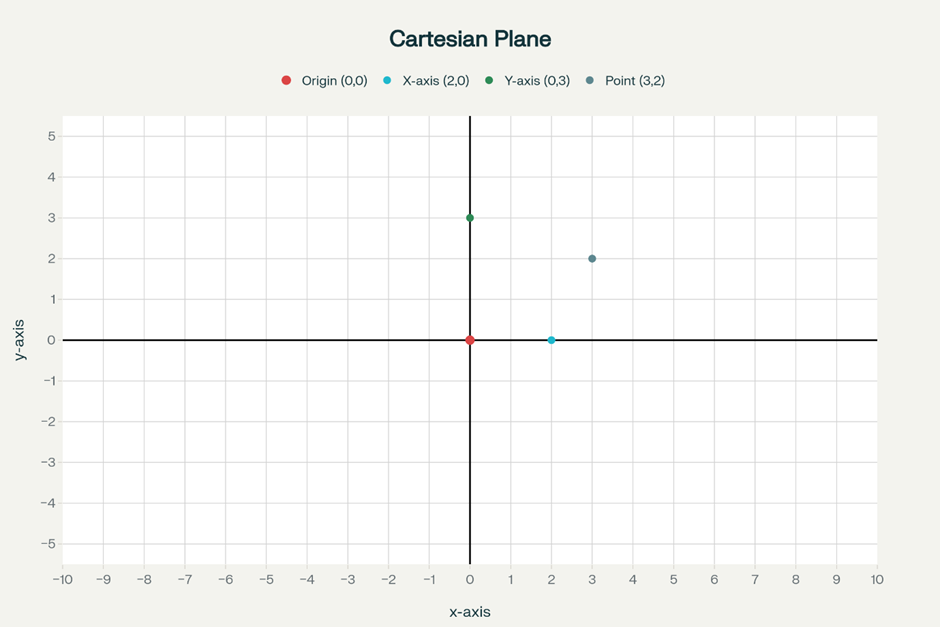
Key Points on the Cartesian Plane and Axes
- Two perpendicular axes are needed to locate a point in a plane: one horizontal (x-axis) and one vertical (y-axis).
- The flat surface these axes lie on is called the Cartesian plane, and the axes themselves are known as the coordinate axes.
- The horizontal axis is called the x-axis; the vertical axis is called the y-axis.
- The intersection point of the two axes is known as the origin.
- The distance of a point from the y-axis is called its x-coordinate (or abscissa). The distance from the x-axis is called its y-coordinate (or ordinate).
- The x-coordinate (abscissa) measures distance from the y-axis, while the y-coordinate (ordinate) measures distance from the x-axis.
- The origin is at zero distance from both axes, so its coordinates are (0, 0).
- Any point on the x-axis has coordinates of the form (x, 0), as it is at zero distance from the x-axis.
- Any point on the y-axis has coordinates (0, y), being at zero distance from the y-axis.
- The axes divide the Cartesian plane into four regions called quadrants.
📏 Linear Equations in Two Variables 📈
An equation of the form ax+by+c=0, where a,b,c are real numbers and a and b are not both zero, is called a linear equation in two variables.
Key Points
- A linear equation in two variables has infinite solutions.
- The graph of every linear equation in two variables is a straight line.
- x=0 is the equation of the y-axis and y=0 is the equation of the x-axis.
- The graph x=a is a line parallel to the y-axis.
- The graph y=b is a line parallel to the x-axis.
- An equation of the type y=mx represents a line passing through the origin.
- Every point on the graph of a linear equation in two variables is a solution of the linear equation. Moreover, every solution of the linear equation is a point on the graph.
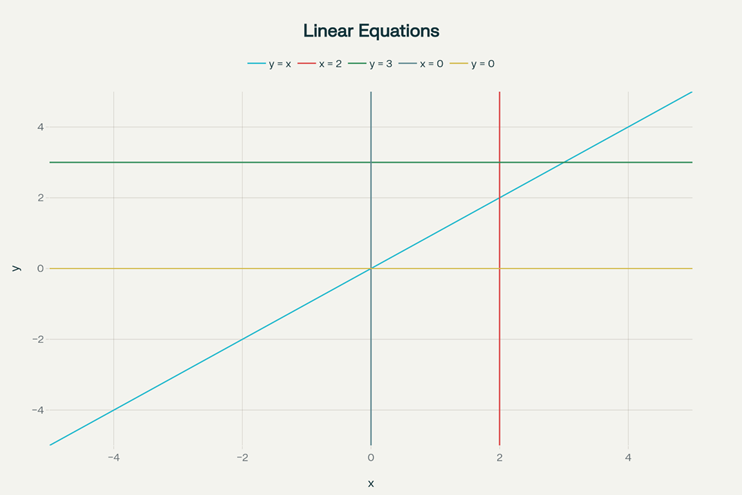
Here is a graph illustrating the key types of linear equations in two variables discussed in the points above. The plot includes:
- y=x (line through the origin, slope = 1)
- x=2 (vertical line, parallel to y-axis)
- y=3 (horizontal line, parallel to x-axis)
- x=0 (the y-axis)
- y=0 (the x-axis)
Each of these lines represents a special case or example mentioned in the extracted key points, demonstrating how every point on each line is a solution to the corresponding equation and each graph is a straight line.
📐 Introduction to Euclid’s Geometry 🏛️
Euclid’s Definitions
- Point – A point is that which has no part.
- Line – A line is breadthless length. The ends of a line are points. A straight line is a line which lies evenly with the points on itself.
- Plane – A surface is that which has length and breadth only. The edges of a surface are curves or straight lines. A plane surface is a surface which lies evenly with the straight lines on itself.
Dimensions of Euclid’s Elements
- A point has no dimensions.
- A line has a dimension of one (1D) because only one coordinate is needed to specify a point on it.
- A surface such as a plane has a dimension of two (2D) because two coordinates are needed to specify a point on it.
- A solid is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.
Euclid’s Axioms
| Axiom | Description |
| Axiom 1 | Things which are equal to the same thing are equal. |
| Axiom 2 | If equals are added to equals, the wholes are equal. |
| Axiom 3 | If equals are subtracted from equals, the remainders are equal. |
| Axiom 4 | Things which coincide with one another are equal. |
| Axiom 5 | The whole is greater than the part. |
| Axiom 6 | Things which are double of the same things are equal to one another. |
| Axiom 7 | Things which are halves of the same things are equal to one another. |
Euclid’s Postulates
| Postulate | Description |
| Postulate 1 | A straight line may be drawn from any point to any other point. |
| Postulate 2 | A terminated line can be produced indefinitely. |
| Postulate 3 | A circle can be drawn with any center and any radius. |
| Postulate 4 | All right angles are equal. |
| Postulate 5 | If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles. |
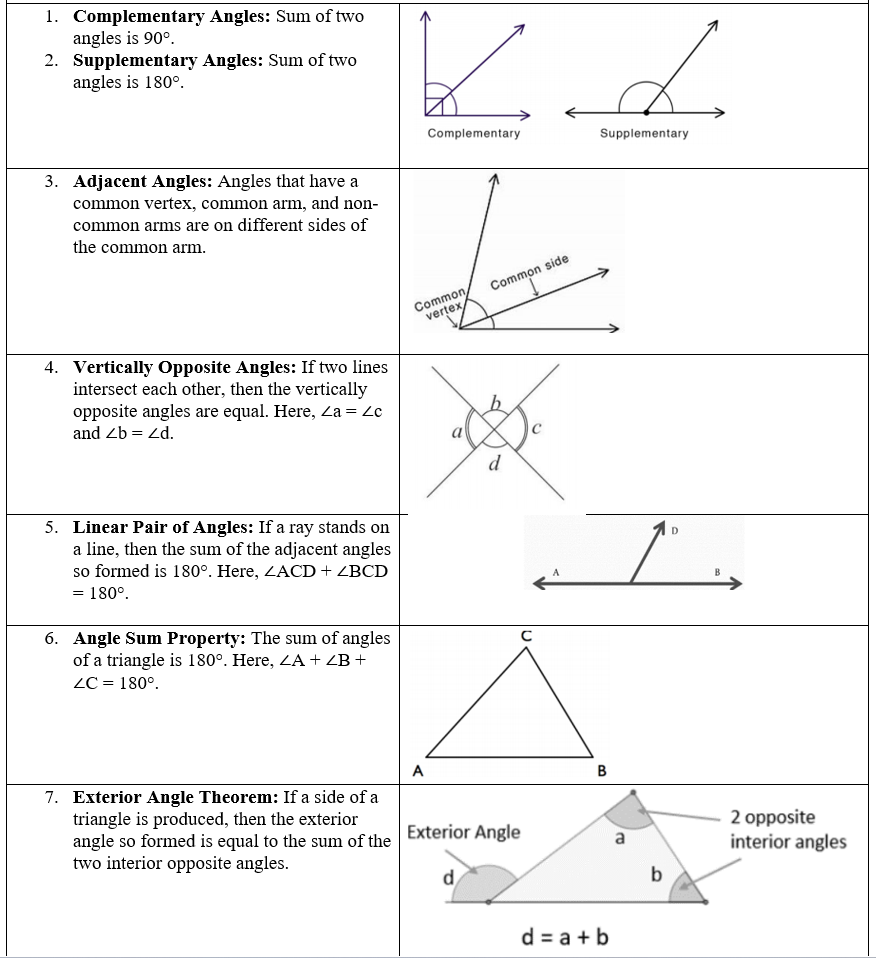
∠ Lines and Angles 📐
ANGLES-
△ Triangles 🔺

▱ Quadrilaterals ⬟
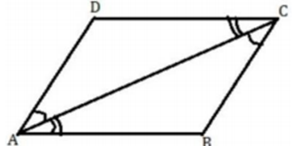
Theorem 1
A diagonal of a parallelogram divides it into two congruent triangles.
Proof: AC = CA ∠BCA = ∠DAC (alternate angles) ∠BAC = ∠DCA (alternate angles)
So, ∆ABC ≅ ∆CDA.
Theorems
- A diagonal of a parallelogram divides it into two congruent triangles.
- In a parallelogram, opposite sides are equal.
- If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
- In a parallelogram, opposite angles are equal.
- If in a quadrilateral each pair of opposite angles is equal, then it is a parallelogram.
- The diagonals of a parallelogram bisect each other.
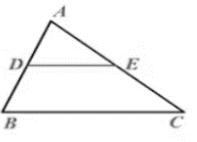
The Mid-Point Theorem
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long. DE = ½ BC ∠ADE = ∠ABC So, EF ∥ BC.
○ Circles 🔄
Chords and Their Properties
- Angle Subtended by a Chord at the Centre Theorem: Equal chords of a circle subtend equal angles at the centre. Converse: If the angles subtended by two chords at the center are equal, then the chords are equal.
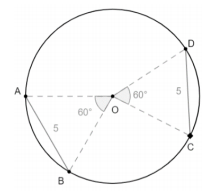
Here, AB = CD and ∠AOB = ∠DOC.
- Perpendicular Bisector of a Chord Theorem: The perpendicular from the center of a circle to a chord bisects the chord. Converse: If a line drawn from the center of a circle bisects a chord, then it is perpendicular to the chord.
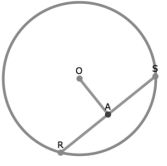
Here, OA ⊥ RS at A and RA = AS.
- Chords and Their Distances
Theorem: Chords of equal length are at equal distance from the center of the circle. Converse: Chords equidistant from the center of a circle are equal in length.
Here, distance of AB and CD from O is equal, so AB = CB.
Angles Subtended by Arc
- Angle Subtended by the Arc of a Circle Theorem: The angle subtended by an arc at the center is twice the angle subtended by it at any point on the remaining part of the circle. Here, ∠AOB = 2 × ∠ACB.
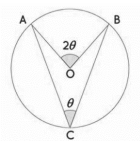
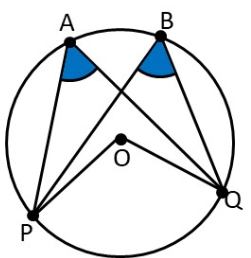
- Angle Subtended in the Same Segment Theorem: Angles subtended by the same arc in the same segment of a circle are equal. Here, ∠PAQ = ∠PBQ.
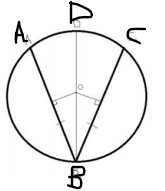
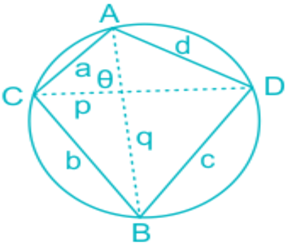
Cyclic Quadrilateral
Theorem: The opposite angles of a cyclic quadrilateral sum to 180°. Here, ∠CAD + ∠CBD = 180° and ∠BAC + ∠BDA = 180°.
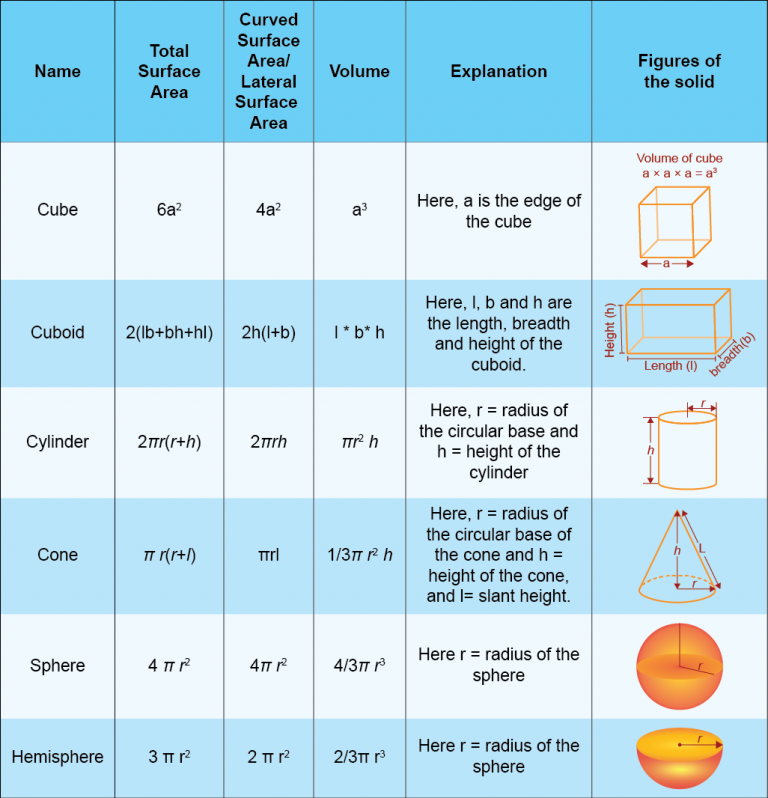
🌐 Surface Area and Volume 🧮
📊 Statistics 📈
Frequency of Data
The number of times a particular value occurs in a data set is known as its frequency.
- Grouped Frequency: Data organized into classes.
| Age (in years) | Frequency (f) |
| 12-15 | 4 |
| 15-18 | 5 |
| 18-21 | 8 |
| 21-24 | 1 |
| 24-27 | 4 |
| 27-30 | 8 |
| 30-33 | 2 |
- Ungrouped Frequency: Individual data values.
| Age (in years) | Frequency (f) |
| 12 | 3 |
| 14 | 8 |
| 18 | 6 |
| 21 | 3 |
| 25 | 5 |
| 28 | 3 |
| 30 | 4 |
- Non-Continuous Grouped Frequency
| Size (cm) | Frequency (f) |
| 34-37 | 4 |
| 37-40 | 14 |
| 40-43 | 6 |
| 43-46 | 8 |
| 46-49 | 3 |
| 49-52 | 4 |
MEAN, MEDIAN, MODE

💡 Special Note from A2zly!
“We believe in providing Free Education, and if this formula booklet has helped you in any way, then you can show your support by just comment in the dropbox. ❤“
There you have it—your all-in-one Class 9 Maths Formula Sheet, ready to fuel your study sessions! Remember, consistency is key: practice these formulas daily, tackle past papers, and watch your confidence soar. If this guide sparked a breakthrough, share it with a friend who’s battling the same chapters. What’s your toughest topic? Drop a comment below—we’d love to hear and help!
Best of Luck! – From the team of A2Zly 🌟

